私の専門は数学のなかでも「確率論」、とくに「確率過程論」とよばれる分野です。身近な例では株価の変動。時間の変化に伴う株価の動きをグラフにすると、ジグザグと不規則な線ができあがります。空中に浮かぶチリもよく眺めてみると予想しない方向に動きながら浮遊していきます。このように何らかの要因(株価であれば社会情勢、空中のチリであれば空気中の見えない小さな粒子との衝突)の影響でジグザグとランダムに動く粒子の運動を数学的に定式化し記述する学問が確率過程論です。
なかでも、今私が対象とするのはチューブのような円柱状の空間内を動く粒子の運動です。たとえば、チューブが縮んだり、潰れたりして形が変わるとき、これまでに知られているモデルでは粒子の動きをうまく捉えられなくなります。そんなとき、どのようにモデルを捉え定式化すると、モデルを記述しその性質を取り出せるのかを考えています。
例えば、交通手段や情報網の発達でウイルスや情報の拡がり方は変化しています。下の絵のように昔は陸続きに伝わっていたものが飛行機やSNSなどを通して拡がり方が変化してきています。このように連続的に伝達(拡散)していたものが、どこかでジャンプを起こしジャンプした先で拡がっていく、また拡散がどこかで消滅するような場合の確率過程の特徴づけと、それに関連する収束定理(連続的に伝わっていていた状況からジャンプが起こるような複雑なモデルへ変化する)の研究を行いました。[▶︎関連論文[1]]、[▶︎関連論文[2]]
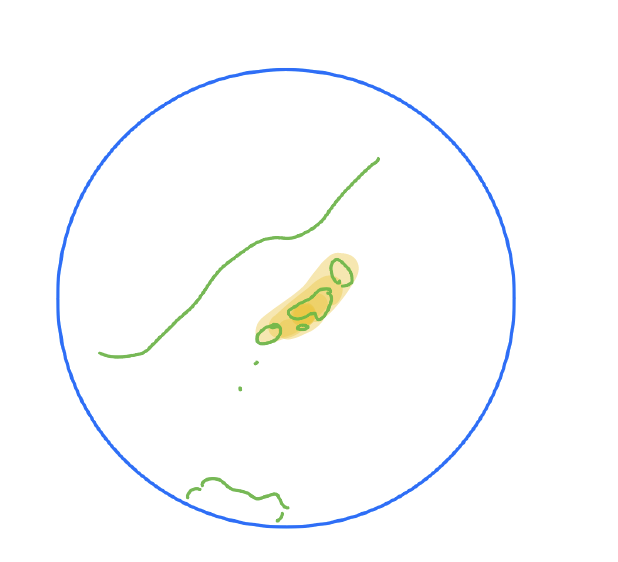
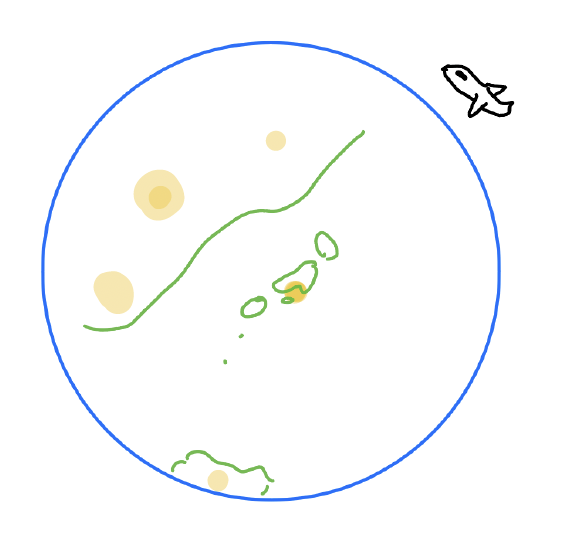
研究をするうえでは、上で挙げたような社会現象を参考にすることはなく、知られているモデルをどこまで複雑に定式化できるか、また条件を緩めることでどのような特異なことが起こりうるのか考えるのが、私の研究の着想です。
最近は、チューブの中をジグザグと動く粒子に興味があり、次のような問題を考えています。



上の絵のようにチューブの中をジグザクに動いているものが、ある部分では観測できなくなってしまったり、またチューブが収縮し、粒子が通りづらい部分ができてしまうような場合のモデルはどのように表現でき、どのような性質をもつのかを研究しています。考えられる条件を書き出し、運動としてどのようなことが起こっているのか、またその運動を記述する関数の性質と睨めっこする毎日です。
数学の理論は、〈公理〉とよばれる前提条件を出発点とします。公理は証明の必要なく「正しい」と定めるもので、理論によっては異なる公理を採用することもあります。つぎに、「○○を○○とする」など、公理という前提のもとで新しく登場させたい概念を〈定義〉します。こうした〈公理〉、〈定義〉のうえになりたつ新しい性質を〈定理〉とよびます。
今私が考えている問題は、血管はチューブのような形をしていますから、私の導き出したモデルは医学や生物学、物理学などのシミュレーションに応用できるかもしれません。とはいえ、いますぐに社会の役にたつかと問われると、答えに詰まるのが本音。でも、数学は、何十年も前の論文を参照しながら、新たな理論を積み上げて定理を証明するものです。私の論文も、何百年と先かもしれませんが、いつかだれかの目に止まれば。そんな思いで数式と向き合っています。
高校生のころまで、勉強が好きではありませんでした.暗記する授業が肌に合わず、「どうしてだろう」と考えるほうが好きでした。試験を受けるときも「設問のここの条件を変えれば、答えが変わりそうだ。そうすればもっとみんな間違えるだろうな」と、パズル遊びのように作問者の気持ちになって楽しんでいました。
地方都市で生まれ育ったからかもしれませんが、「数学科に進学した」という知り合いもなく、数学を専門に学ぶ学科があることすら知りませんでした。ある日、通っていた予備校で数学科出身の先生と出会ったのがターニングポイント。大学の数学には、決まった答えがないだけでなく、そもそも問題を自分で設定して考えてゆくものだと知ったのです。私がふだん、数式を前にあれこれ思い巡らせていたことは学問の入り口だったのだと、雷が落ちたような衝撃を受けました。
中高生に数学のおもしろさがきちんと伝われば、当時の私のように数学を好きになれる学生もいるのではないか。そう思い立って、日本各地の数学科の大学教員の有志といっしょに「数理女子」というウェブサイトを運営しています。身近で数学が役だつ例や、数学を学んだ先に拓く進路、数学研究者の日常を紹介して、数学に親しんでもらおうというねらいです。
数学者というと、もくもくとノートや黒板に向かうイメージがあるかもしれませんが、研究を大きく前進させるには、ほかの数学者との議論から生まれるアイデアが不可欠。私にとっても、国内外の研究者と数学のむずかしさに共感しあい、おもしろさ美しさを共有しながら議論したことで、より数学の世界に魅せられました。
学部で数学を学んでも、修士課程に進学する学生はそれほど多くない現状があります。大学院に進学する学生が増えれば、数学研究はさらに活発になるのです。
国立大学で数学の修士号を取得する女子学生の数は、毎年70人から100人。奈良女子大学の数学科は進学率が高く、毎年約10人が修士課程に進みます。日本で数学の修士号をもつ女性の約15%は奈良女子大学の卒業生だといえるかもしれません。
数学の世界にはおもしろいことがまだまだたくさんあって、すべてに取り組むには時間が足りません。私にとって数学研究は、地平線はもちろん、その先がどこにつながっているのかも見えないまま、海の中を漂うようなもの。でも、それがとにかく楽しい。最期の日まで数学をつづけるのが私の夢です。

「数理女子」活動をともにする数学者と、日常のなかにある数学のおもしろさをわかりやすく発信。〈嶽村智子、大山口菜都美、酒井祐貴子『めくるめく数学。』(明日香出版社、2023年)〉
「こんなことをおもしろがっている人もいるんだ」とだれかの目に止まり、数学という学問の世界にふれるきっかけになることを期待しています。高校生のころの私のように、「数学」をまだ知らない学生に届いてほしいです。