FAX 0742-20-3367 email shinoda@cc.nara-wu.ac.jp
研究集会「無限粒子系、確率場の諸問題」（2005年度より年１回開催）のご案内
→研究集会「無限粒子系、確率場の諸問題XX」（2026年1月24日-25日、於奈良女子大学）
→研究集会「無限粒子系、確率場の諸問題XIX」（2025年1月25日-26日、於奈良女子大学）
→研究集会「無限粒子系、確率場の諸問題XVIII」（2024年1月20日-21日、於奈良女子大学）
→研究集会「無限粒子系、確率場の諸問題XVII」（2023年1月21日-22日、於奈良女子大学）
→研究集会「無限粒子系、確率場の諸問題XVI」（2021年10月16日-17日、於奈良女子大学）
→研究集会「無限粒子系、確率場の諸問題XV」（2020年1月25日-26日、於奈良女子大学）
→研究集会「Stochastic Analysis, Random Fields and Integrable Probability」（2019年7月31日-8月9日、於九州大学椎木講堂）
→研究集会「無限粒子系、確率場の諸問題XIV」（2019年1月26日-27日、於奈良女子大学）
→研究集会「確率解析の諸相」（2018年1月5日-6日、於九州大学西新プラザ）
→研究集会「無限粒子系、確率場の諸問題XIII」（2017年11月25日-26日、於奈良女子大学）
→研究集会「無限粒子系、確率場の諸問題XII」（2017年1月21日-22日、於奈良女子大学）
→研究集会「無限粒子系、確率場の諸問題XI」（2015年12月26日-27日、於奈良女子大学）
→研究集会「無限粒子系、確率場の諸問題X」（2014年11月29日-30日、於：横浜情報文化センター）
→研究集会「無限粒子系、確率場の諸問題IX」（2014年1月11日-12日、於：奈良女子大学）
→研究集会「Recent topics on Markov processes」（2013年2月10日、於：奈良女子大学）
→研究集会「無限粒子系、確率場の諸問題VIII」（2012年10月20日-21日、於：奈良女子大学）
→研究集会「非正則な拡散過程における諸問題」（2012年1月29日、於：奈良女子大学）
→研究集会「無限粒子系、確率場の諸問題VII」（2011年10月15日-16日、於：奈良女子大学）
→研究集会「ジャンプ過程における諸問題」（2011年1月9日、於：奈良女子大学）
→「第24回ゲーム情報学研究会」（2010年6月25日）会場案内
→研究集会「統計力学の数学的理論」（2009年8月24日-25日）
→国際研究集会「大規模相互作用系の確率解析」（2007年10月22日-26日）
確率論
自然現象などに対応する確率モデルを作り、その性質を調べています。
流体を例にとって説明します。１個１個の分子がでたらめな動きをしても、多くの分子全体を見れば平衡状態であったり、あるいはひとつの流れであったりします。それぞれの分子の挙動をモデル化し、全体の動きを「大数の法則」や「中心極限定理」でつかむことが考えられます。この２つの定理は、確率論の講義で勉強するものです。
私は特にパーコレーションという問題を研究しています。これは相転移現象（氷が０℃で水に変化する、など）を表す確率モデルです。臨界点が１つかどうか、またその臨界点でどのような相転移を起こすかなどという問題が、モデルの設定とどのように関連しているかを調べています。
ゲーム情報学
数学的構造を含むゲーム全般に興味があります。
囲碁、将棋、麻雀、バックギャモン、ポーカーなど人々に楽しまれているゲームはさまざまです。こうしたゲームは運の要素を含むものや含まないもの、目標も勝つことや利得を最大にすることなど様々です。私はこうしたゲームの「戦略」について研究しています。
こうした研究の対象は娯楽であるゲームだけではありません。人々の社会行動の多くは数理モデル化によってゲームになぞらえることができます。こうした広い意味での「ゲーム」について、適切な行動や互いの協力関係について調べています。
パーコレーション、フラクタル、相転移現象、数理ゲーム、組合せゲーム理論
M.Shinoda, E.Teufl and S.Wagner, Uniform spanning trees on Sierpinski graphs,
Latin American Journal of Probability and Mathematical Statistics Vol.11 (2014), 737-780.
H.Oginuma, M.Shinoda, Shrinking Circular Nim, To appear in Journal of Information Processing Vol.33 Dec. (2025).
M.Shinoda, Existence of phase transition of percolation on fractal lattices, COE Lecture Note Series, Instisute of Mathematics for Industry, Kyushu University, Vol.39 (2012), 12-21.
M.Shinoda, Y.Sakurai and S.Oyama, Sample Complexity of Learning Multi-value Opinions in Social Networks, PRIMA 2022: Principles and Practice of Multi-Agent Systems, the series Lecture Notes in Computer Science 13753 (2023), 192-207.
R.Yoshioka, Y.Sakurai, S.Oyama, M.Shinoda, Proposing a New Security Game with Reward and Penalty, 2023 IEEE International Conference on Web Intelligence and Intelligent Agent Technology (WI-IAT) (2023), 205-212.
Y.Sakurai, M.Matsuda, M.Shinoda, S.Oyama, Crowdsourcing Mechanism Design, PRIMA 2017: Principles and Practice of Multi-Agent Systems, the series Lecture Notes in Computer Science 10621 (2017), 495-503.
Y.Sakurai, T.Okimoto, M.Oka, H.Hyodo, M.Shinoda and M.Yokoo, Quality-Control Mechanism utilizing Worker's Confidence for Crowdsourced Tasks Proceedings of the Twelfth International Conference on Autonomous Agents and Multiagent Systems (AAMAS2013).
荻沼弘実, 篠田正人, 3山得点付きニムの利得関数，ゲームプログラミングワークショップ2024論文集 (2024), 1-8.
荻沼弘実, 篠田正人, 収縮円形ニム, 情報処理学会研究報告 Vol.2024-GI-51, No.7 (2024).
荻沼弘実, 篠田正人, Nimの拡張となる石取りゲームの提案, 情報処理学会研究報告 Vol.2024-GI-52, No.7 (2024).
安福智明，坂井公，篠田正人，末續鴻輝, 分割削除ニムの勝敗判定，ゲームプログラミングワークショップ2022論文集 (2022), 17-24.
吉岡陸, 櫻井祐子, 小山聡 , 篠田正人, 報酬と失敗コストを導入した数当てゲーム，ゲームプログラミングワークショップ2022論文集 (2022), 25-28.
安福智明，坂井公，篠田正人，末續鴻輝, 拡張削除ニム，情報処理学会研究報告GI-48, No.14 (2022).
篠田正人, Delete Nimの一般化と勝敗判定，情報処理学会研究報告GI-47, No.5 (2022).
杉山悦子, 篠田正人, A Cat-and-Mouse game on the set of integers, 情報処理学会研究報告GI-38, No.4 (2017).
篠田正人, 3*N AB gameにおける最適戦略, 情報処理学会論文誌ジャーナル, Vol.53, No.6 (2012), 1-8.
篠田正人, 人間側から見るコンピュータ将棋の強さ, 知能と情報（日本知能情報ファジィ学会誌）Vol.26, No.5, (2014), 204-211.
T.Abuku, K.Sakai, M.Shinoda, K.Suetsugu, Some extensions of Delete Nim, arXiv:2301.12964 (2023).
M.Shinoda, Single-delete Nim, arXiv:2411.19453 (2024).
H.Oginuma, M.Shinoda, Scoring Nim, arXiv: 2502.10971 (2025).
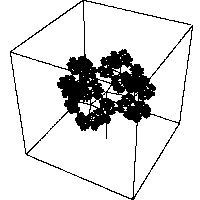
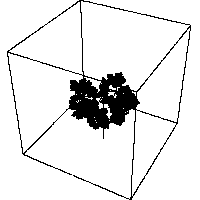
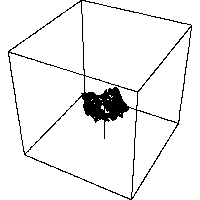
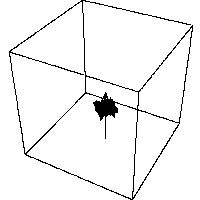
Self-contacting fractal tree in three dimensions, joint work with M.NAKAYAMA.