算額にチャレンジ(解答編)
ー問題4ー
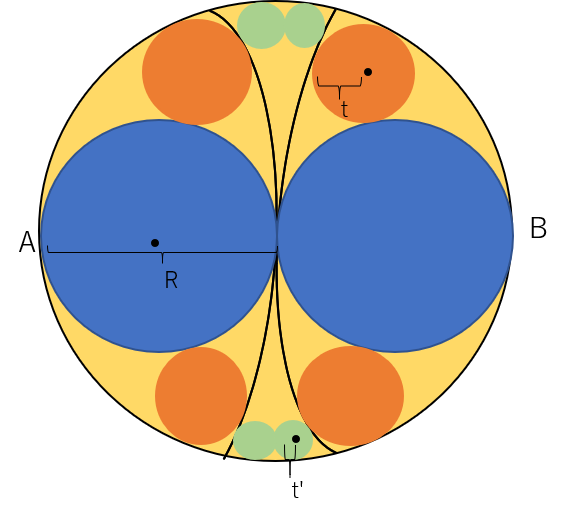
直径がAB=2Rの円に、中心をAとBとして半径がRの円弧を引く。そして半径R/2の二つの大円(あお色)、半径tの四つの小円(オレンジ色)、半径t’の四つの小円(きみどり色)でなる10個の円が図のように接している。この時t=t'=$\frac{R}{6}$を確かめる。
解法
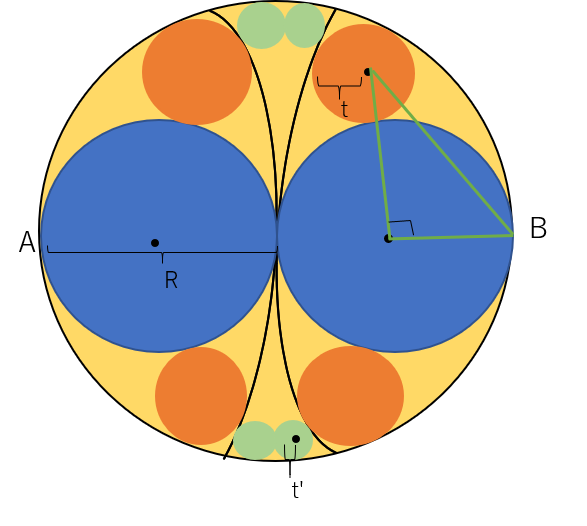
図1-1
まず、図1-1のようにBと半径tの小円(オレンジ)の中心と半径$\frac{R}{2}$の大円(あお)の中心を結ぶと直角三角形ができるので、三平方の定理が利用できる。
よって、 \begin{align*} (R-t)^2=& (t+\frac{R}{2})^2+\frac{R}{2} ^2\\ R^2-2Rt+t^2=& t^2+Rt+\frac{R}{2}^2\\ t=& \frac{R}{6}\\ \end{align*}
次に、図のようにAと半径t’の小円(きみどり)の中心と半径Rの大円(き)の中心を結んだ三角形を考え、図のように$\theta$をおく。
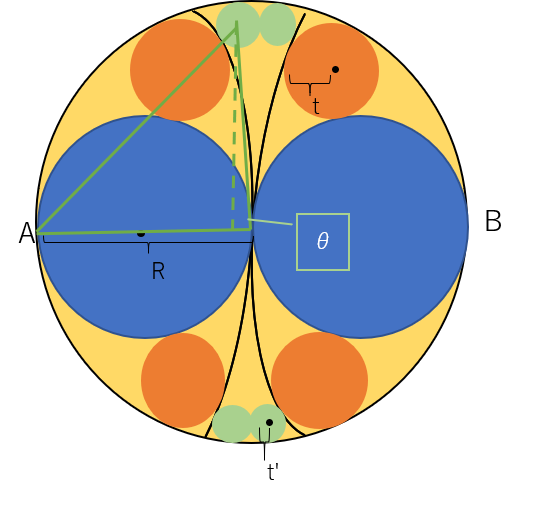
図1-2
三角関数の性質より

図1-2