最新の研究紹介

[ リリース： 2015.11 ]
奈良女子大学理学部 数物科学科 物理学コース・数物連携コース兼担　上江洌達也

　研究の紹介というと、通常は無味乾燥な式の羅列になってしまいがちで、専門家以外にその内容を伝えることはなかなか難しい。本稿もその誹（そし）りを免れ難いと考えたので，通常とは異なり、最初に研究分野の概説を行い、そのあと、具体的な研究の紆余曲折を述べよう。

　着目している系において、温度が一定になりすべての物理量がほぼ一定の値をとっている平衡状態の記述は、現象論としての熱力学として確立し、ついで微視的立場から記述する平衡統計力学がギブズらによって打ち立てられた。ところが、平衡状態からかなり離れた場合には、非平衡状態そのものをまともに取り扱う必要があり、未だ一般論は存在しない。非平衡状態は多種多様であり、その各々において個別の研究が行われ、非平衡系へのアプローチは色々であるが、その一つとして現象論的方程式から出発するという立場がある。我々はこの立場で研究を行っている。

　ここで取り上げる非平衡現象はリズム現象である。心臓の拍動、流体における対流、概日周期（サーカディアンリズム）、化学反応における振動（BZ反応など）など、自然界は振動現象に満ちている。我々は、振動している多数の素子が相互作用することによって、バラバラな振動から同じ振動数で振動するようになる現象、すなわち、同期現象を研究対象とする。これは、非平衡系の相転移と考えることができる。

　各振動子の振動は微分方程式で記述されるとする。もし、振動子間の相互作用の大きさが小さければ、この系は各振動子の位相のみの微分方程式系で記述できることが分かっている。これは、位相振動子モデルと呼ばれている。我々は、相互作用項をサイン関数にした次の微分方程式系を扱う。



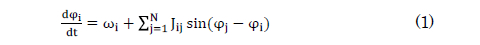
　ここで、φ_iはi番目の振動子の位相、Nは振動子の数、Jijはj番目の振動子がi番目の振動子に及ぼす影響（相互作用）の強さ、 ω_iは自然振動数で、g(ω）を自然振動数の散らばり具合を表す関数とする。もし自然振動数が一定で相互作用が対称（Jij=Jji）であれば、この系は同一の相互作用を有する温度０の古典XYモデル（磁石のモデル）と同等であることが分かる。これが我々の研究の出発点である。

　式(1)で、相互作用が一定とした系は、蔵本由紀氏が同期非同期転移を始めて解析的に示し、蔵本モデルと呼ばれ夙（つと）に有名である。概略を述べると、相互作用の強さがある値よりも大きい、あるいは自然振動数のばらつきがある値よりも小さいと、バラバラな振動から多数の振動子が同期する現象が起こる。我々は、蔵本モデル以外で解くことのできる位相振動子モデルを構築することを目指した。そのために、1次元系ではあるが各振動子が他の全てと相互作用する系を取り上げた。系が同期している度合いを示す量は、秩序パラメータと呼ばれ、今の場合は複数個の複素数である。蔵本モデルでは秩序パラメータは１個のみで、その位相部分は自然に消去され、振幅のみの式となったのであるが、今のモデルでは位相部分も求める必要がある。一方、同一の相互作用を有するXYモデルは古典統計力学の範囲で解けるので、その位相の情報を用いることにした。回り道ではあるが、解くための方策としてXYモデルの研究も行ったのである。結果からいうと、これは実にクリエイティブな回り道であった。これによって位相の情報が得られたので，それを用いて振幅の式を求め相図を描いた（下右図）。



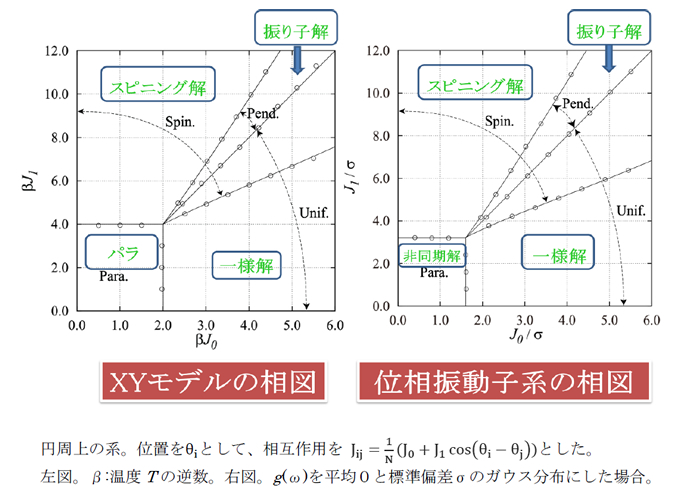
　ついでに、XYモデルの相図も描くと左図のようになった。両系の相図は極めてよく似ているが、さらに、振幅の方程式も似ていることが分かった。相図の境界の式も解析的に求められるがそれも似ている！ただ、その時は深い意味があるとは思わず、学会で発表した際にも特にコメントはなかった。ところがあるとき、位相の従う方程式の導出方法が分かった。分かってみれば当たり前に思えるのはいつものことである。しかも位相の式も両系で似ているではないか！相転移点の対応関係も分かり、自然振動数のばらつきの幅と温度が対応することも分かった。そこで、方程式だけでなく解も対応するのではないかと本気で考え始めたのである。そして、いくつかの試行錯誤の後に、解が1対１に対応することを数学的に厳密に証明することができた。秩序相は3つあり、いずれの相においても解が１対１に対応する。また、相境界の式も対応する。対応が成り立つ相互作用も拡張され、全てと相互作用するあるクラスの系であれば、方程式が１対１に対応することを示すことができた。また、解の対応もいくつかの場合で示された。これらの結果は、論文として、学術雑誌Journal of Physical Society of Japan に掲載された（Journal of the Physical Society of Japan in February 2015）。そして、1946年の創刊以来掲載された全論文中、2015年2月の Most Downloaded Top 20 Articles（もっともダウンロード回数が多い論文のトップ２０）に入った。

　クリエイティブな間違いの例はいくつか知っていたし、クリエイティブな回り道も当然多々あるだろうとは思うが、回り道のおかげで予想もしなかった発見をしたのは初めての体験であった。

[1] Correspondence between Phase Oscillator Network and Classical XY model with the Same Infinite-Range Interaction in Statics
Tatsuya Uezu, Tomoyuki Kimoto, Shuji Kiyokawa, and Masato Okada J. Phys. Soc. Jpn. 84, 033001 (2015)