数学コースのHP(新着情報はこちら) 関連する大学院→ 博士前期課程 数学コース
数学ってどんな分野?
数学者カントル(Cantor)は「数学の本質はその自由性にある」と主張しました。この言葉の通り、この世に存在するあらゆる事象は数学の対象になります。数学は、複雑な事柄から普遍的な法則を引き出し、また逆に簡単な原理から理論を展開し深化させる学問です。数学の真理は様々な学問の基礎となり、時代を超え、形を変えて多彩な発展を遂げ、古今東西を問わず多くの人々を魅了し続けています。
具体的には以下で紹介しますが、現代数学はまず微分、積分、ベクトル、行列、集合といった基礎の上に立脚しています。そして、代数学、幾何学、解析学などの様々な分野に枝葉を広げていきます。また、論理的思考だけでなく、数学的感覚も大切です。社会生活の様々な場面においても、幅広く活用できる思考や感覚です。学問は常に発展し、変化し続けています。数学もその例外ではありません。
教育に対する考え方

数学の講義風景
数学コースでは、まず微分、積分、ベクトル、行列、集合といった現代数学の基礎を講義・演習を通してしっかり教育し、学生の数学的思考や感覚を育てます。さらに専門性の高い発展的科目へと進ませ、様々な対象を深く観察しその構造の全体を捉える力、論理的に物事を解析する力、明晰な言葉で論証し表現する力を学生に身に付けてもらいたいと考えています。職業生活や社会生活の様々な場面においても、これらの能力を幅広く活用できる人材を育てることが数学コースの教育目標です。
さらに数学コースでは、分野横断的な学科共通の授業科目を受講させることにより、より広い視野から自然現象を理解し、領域横断的な状況に直面しても柔軟に問題に対応し解決することができる人材を育てることも目標としています。
学問は常に発展し、変化し続けています。単に既成の数学を教えるというのではなく、発展しつつある数学を教員・学生がともに体験し、互いに研鑽していく中で、これらの能力を伸ばしていきたいと考えています。
求める学生像

図書室での勉強風景
大きく変動する時代の中で本質が何かを見極めたいという好奇心や探究心にあふれた人が来て下さることを期待しています。柔軟で生き生きとした感受性を持った皆さんと、現在も発展しつつある数学をともに体験し、互いに研鑽していきたいと願っています。数学コースを希望される皆さんには特に高校数学の内容をしっかりと身につけておくことを希望します。
教育・研究分野
数学の教育や研究は、個別的なものではなく総合的なものです。
種々の対象にどのような構造が存在し、それらが相互にどのように関連しているかを研究し、それによって対象の構造の全体をとらえることを目的としています。幾何学、代数学、複素解析学といった分野の研究教育を中心とし、さらにこうした従来の枠にとらわれずに数学的構造に関する新しい知識を得ることも目指しています。
また、さまざまな現象における変化・変動のメカニズムを、微分積分学をもとに研究し、深く理解することを目的としています。確率論、非線型解析、実解析、数論といった分野の研究教育を中心とし、さらに相互作用させることによって現象解析の一層の進化と豊かな発展を目指しています。
以下にその一部を、図や式を交えて紹介します。

教員スタッフ一覧
カリキュラム
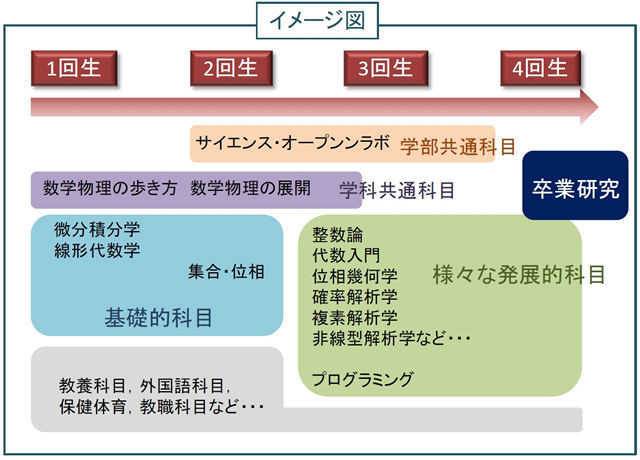
数学コースでは、まず前半に微分、積分、ベクトル、行列、集合といった現代数学の基礎を講義と演習を通してしっかり学習し、数学的思考や感覚を身に付けます。後半では、代数・解析・幾何などの、現代数学の様々な分野への入門的な科目を通して、より専門性の高い内容を学びます。また、プログラミングなどのコンピュータの扱いに関する科目も履修できます。最終学年では少人数でのセミナーを行い、自分で進んで知識を取り入れ、研究を進め、発表を行います。
さらに数学コースでは、より広い視野から自然現象を理解し、領域横断的な状況に直面しても柔軟に問題に対応し解決することができる人材を育てることを目標として、学科共通の分野横断的な授業科目を受講してもらいます。
数学コースのHP(新着情報はこちら) / 関連する大学院→ 博士前期課程 数学コース







