最新の研究紹介

[ リリース： 2018.10 ]
奈良女子大学 理学部 数物科学科
教授　小林毅、准教授　張娟姫、准教授　村井紘子

トポロジー(topology)は位相幾何学とも呼ばれる数学の一分野で、「図形を伸ばしたり縮めたりしても変わらない性質を考える幾何学」と呼ばれています。トポロジーが一般的にイメージされる幾何学と異なるのは、図形の大きさや長さ、角度、曲率などといった定量的な側面に焦点を合せるのではなく、例えば成分の数や穴の数といった「定性的な図形の特徴を調べる」という点にあります。

さて奈良女子大学には小林毅、張娟姫、村井紘子の3名のトポロジスト（トポロジーの研究者のことをこのように呼びます）がいるほか、山下靖教授、船越紫特任助教もトポロジーの研究を行っています。この他にも大学院生などにトポロジーの研究者が在籍しており大きなグループを作っていて全体として緩やかにつながりを持ちながら各自の研究を進めています。なおこのグループが主に研究しているテーマは「低次元トポロジー」、特に「3次元多様体論」や「結び目・絡み目理論」と呼ばれるものです。（ここで、「低次元トポロジー」と言うのは「３または４次元のトポロジー」という意味です。5次元以上のトポロジーと３、４次元のトポロジーはまったく研究の方法が異なるために、このように区別されています。）今回はこの奈良女子大学トポロジーグループの最近の研究活動についてご紹介したいと思います。

３次元多様体とポアンカレ予想
3次元多様体と呼ばれる空間についてお話ししたいのですが、まずは簡単に目に見える2次元多様体から始めることにしましょう。2次元多様体というのは例えばボールの表面（トポロジーでは「2次元球面」と言います）や浮袋の形（「トーラス」と言います）のような図形のことです。このような図形は、その上のどこの点をとっても、その近くは円板の形をしています。逆にこのように「その上のどこの点を取ってきても、その近くは円板の形をしているような図形」のことを2次元多様体といいます。このような図形は2次元球面やトーラスのように「目に見える」ものだけではなく「クラインの壺」と呼ばれる、直接目にすることはできないような図形もあります。ではこの考え方を3次元に持ち上げてみましょう。3次元多様体と言うのは各点の周りが3次元座標空間のようになっているような空間のことです。例えて言うなら、3次元多様体の研究とは「宇宙の形がどのようになっているのか研究している」という感じです。

３次元多様体はトポロジーの重要な研究対象ですが、奈良女子大学では３次元多様体に関連した先端的な研究が行われています。（以下の話には専門的な言葉が出てきますが、細かい用語などは気にせず雰囲気を感じていただければ、と思います。）

ところで、皆さんは「ポアンカレ予想」という問題をご存知でしょうか。これは今から100年以上も前にフランス人数学者ポアンカレが提案し、2002年頃にロシア人数学者ペレルマンによって解決されました（これは現代数学の記念碑といえる結果です。その内容については 参考文献１にまとめられていますので興味のある方はご覧ください）。ポアンカレ予想がどういう問題か、をちゃんと説明するのは難しいのですが、（用語の意味がわからないことは置いておいて）とりあえず次のように表現されます。

ポアンカレ予想：与えられた3次元多様体の中にあるすべての「輪っか」を一点まで縮めることができるならば、その３次元多様体は３次元球面（中身の詰まったボールを２個、表面で貼り合わせた３次元多様体）になるだろう。

ところで「その３次元多様体の中にあるすべての輪っかを一点まで縮めることができる」ことをトポロジーでは「基本群の生成元の数が０である」と表現します。つまりポアンカレ予想は、次のように言い換えることができるのです。

ポアンカレ予想：３次元多様体Mの基本群の生成元の数が０であるならば、Mはボール２個を貼り合わせて得られるだろう。

ここでこの問題を一般化することを考えます。まずここに出てきた「ボール」の代わりに、ボールに次のような「取っ手」（数学的には「ハンドル」と呼ばれています）をn個つけてできる、n人乗りの浮袋の形（ただし，中身は詰まっています）をした図形のことを「種数nのハンドル体」と言います。特に「ボール」は「種数０のハンドル体」と呼ぶことにします。すべての３次元多様体は、「種数nのハンドル体を二つ持ってきてその表面を貼り合わせることによって得られる」ことが知られていますが、この分解は、その提唱者にちなんで，Heegaard分解と呼ばれています。この表現を使うとポアンカレ予想は更に次の形に言い換えることができます。

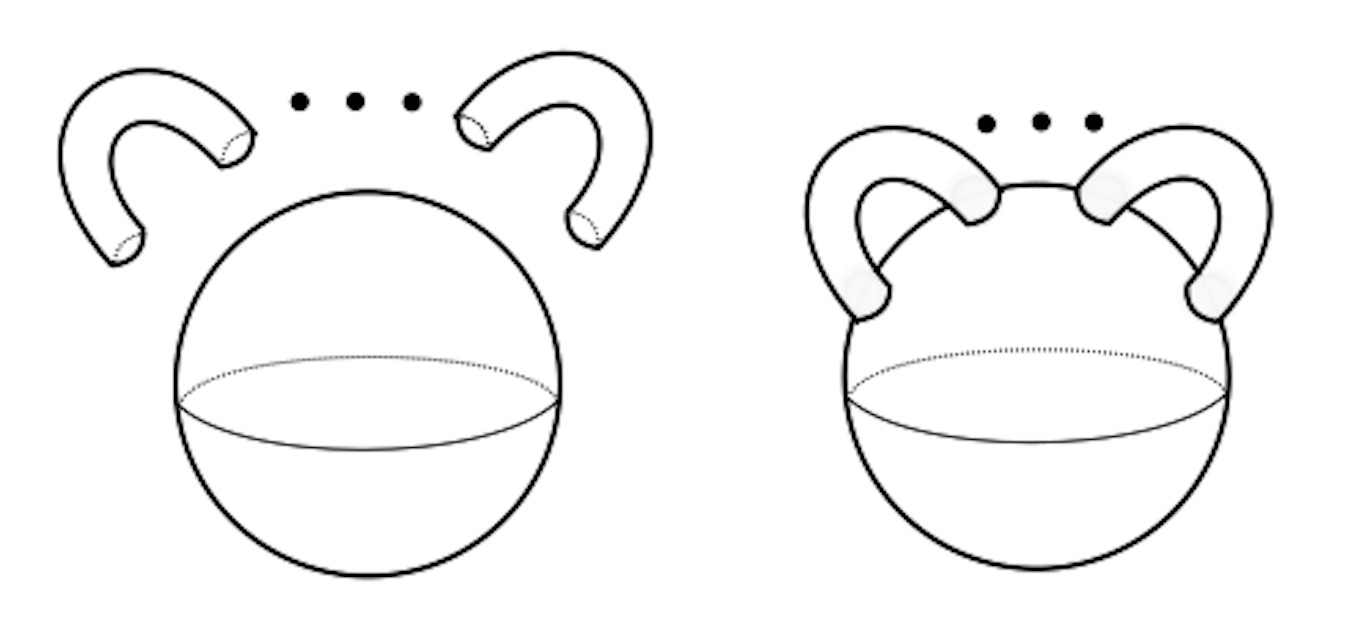
種数nのハンドル体

ポアンカレ予想：３次元多様体Mの基本群の生成元の数が０ならば、Mは種数０のハンドル体からできるHeegaard分解を持つだろう。

なんだか問題の中に数字の０が２回出てきましたね。この部分に注目してやるとポアンカレ予想は次のように一般化することができます。

一般化されたポアンカレ予想：３次元多様体Mの基本群の生成元の数がnならば、Mは種数nのハンドル体からできるHeegaard分解を持つだろう。

この問題は否定的な解答も含めていろいろ興味深い事実と関連していることが知られており、もともとのポアンカレ予想が解決された現在でも、依然として興味がつきません。これに関連して張はBoileau, Weidmannらと共同でこの問題の類似を絡み目の外部空間に対して研究しています。参考文献２ではハンドル体の種数の類似である「絡み目のメリディアン的階数」と呼ばれる量による定式化を取り扱っておりこの一般化されたポアンカレ予想に対して部分的に肯定的な結果を与えています。

またこのHeegaard分解はそれ自体興味深い研究対象で、小林と張はこれに関する研究を行っています。３次元多様体のHeegaard分解に関しては1987年小林が提案したハンドル体上のループの「高さ」という概念に触発され2001年にHempelが「距離」（現在は「Hempel距離」と呼ばれています）を定義しました。これは曲線複体と呼ばれる空間内で二つのハンドル体が作る円板複体の間の距離として定式化されるものですが、小林と張は、本学の大学院の修了者である井戸絢子（2018年現在愛知教育大学）と共同でこの距離を実現する最短曲線に更に強い条件をつけた「keen（鋭い）Heegaard 分解」と呼ばれる概念を提案し、これに関する結果を得ています。参考文献３で、このようなHeegaard分解が豊富に存在することを示しています。その後この研究は、結び目の絡み目の橋分解と呼ばれる分解に拡張されるなど現在も発展を続けています。

結び目や球面曲線の研究
空間の中でひもを結んでできる「結び目」や「絡み目」と呼ばれる図形は低次元トポロジーの困難さと面白さを集約したような重要な研究対象です。結び目・絡み目に関する研究は数学にとどまらず物理学や生物学においても重要性が認められています。特に物理学の観点から結び目・絡み目を点の生成，運動，消滅といった一連の動きとみなした新たな視点（「位相的場の理論」と呼ばれています）が導入され、これをもとに様々な方面に研究が発展しています。（この辺の事情については参考文献４に現代的な観点から要領よくまとめられています。なお、この本の中には奈良女子大学の関係者の名前がたくさん出てきますので、もし本を手にする機会があったら探してみてください。）そのような研究の一つに球面曲線の、ある関係のもとでの同値性に関する問題があります。小林は村井と共同で、この観点を更に一歩進めて、球面曲線からある複体を構成し、そこから定まる距離に関する評価式を得ることに成功しています（参考文献５）。

折紙の数学
「折紙が低次元トポロジーと関係するのか？」と疑問に思われる方もいると思いますが、まずは次の左の図を御覧ください。

これは「2次元トーラス上の相似構造」と呼ばれるものを展開して得られる図形の各辺に赤と緑の色をつけたものです。この赤い辺を山折、緑の辺を谷折りにしてやると右の写真のような、お花に似た形をした折り紙ができます。さて数学者Thurstonは1970年代終わりごろに３次元多様体に関する講義録を出版しましたが、これはこの分野の研究を新しい段階に一気に引き上げるとともにこの分野の研究の方向性を決定づけたといえる重要な文献です（Thurstonの研究については上記の書籍（参考文献１）に詳しく紹介されています）。２次元トーラス上の相似構造とはこの講義録の中で「双極的なデーン手術」と呼ばれている概念を定式化するために導入されたものなのです。小林と村井はこの相似構造を利用して上のような折り紙を組織的に構成する方法を与えました（参考文献６）。このような観点を取り入れることにより、コンピュータを使って、類似の折り紙を大量に作り出すことができるようになりました。


以上、奈良女子大学のトポロジーグループでごく最近行っている研究の中で代表的なものを紹介しました。奈良女子大学トポロジーグループの活動についてはFacebook でも発信していますので、興味のある方はそちらもご覧ください。
https://www.facebook.com/NWUTopologyGroup/

また小林によるトポロジーの紹介記事があります。よろしければそちらも御覧ください。
https://lab-on.jp/academia/122/

参考文献

１．市原一裕，「低次元の幾何からポアンカレ予想へ　世紀の難問が解決されるまで」（技術評論社）2018年

２．Michel Boileau, Yeonhee Jang and Richard Weidmann, "Meridional rank and bridge number for a class of links", Pacific J. Math. 293(2018), no. 1, 61-80.
（https://arxiv.org/abs/1510.00816）

３．Ayako Ido, Yeonhee Jang, Tsuyoshi Kobayashi, "On keen Heegaard splittings", Adv. Stud. Pure Math. 78 (2018), 293-311.

４．伊藤昇，「結び目理論の圏論 「結び目」のほどき方」（日本評論社）2018年

５．Yukari Funakoshi, Megumi Hashizume, Noboru Ito, Tsuyoshi Kobayashi, and Hiroko Murai, "A distance on the equivalence classes of spherical curves generated by deformations of type RI", Jour. Knot Theory and its Ramifications, Vol.27, No.12, 1850066, 2018.

６．Miki Irii, Tsuyoshi Kobayashi, and Hiroko Murai, "Similarity structure on 2-dimensional torus and flat origami", JP Jour. of Geometry and Topology, 22(2019), 45―63.