Correspondence between the Synchronization of an Oscillator Network and the Emergence of Magnetism EA Creative Detour
 [Release: November, 2015]
[Release: November, 2015]
Professor Tatsuya Uezu
Course of Physics, Course of Physics and Mathematics
Department of Mathematical and Physical Science
Faculty of Science
Nara Women's University
First, we provide an overview of our field of research. We then follow up with details on our research.
In a given system, an equilibrium state (i.e., the temperature is uniform and all physical quantities have a nearly uniform value) can be described by thermodynamics, which is a phenomenological theory. From a microscopic point of view, the equilibrium state can be described by equilibrium statistical mechanics established by Gibbs and others . However, although non-equilibrium states must be treated appropriately, a general theory that serves this purpose has yet to be established. Non-equilibrium states are diverse, and different studies use different approaches to non-equilibrium systems. One of these approaches is to start from a phenomenological equation. We pursued our research from this standpoint.
Here, we discuss the non-equilibrium phenomenon of rhythm. The natural world is filled with oscillatory phenomena: heartbeats, convection in a fluid, circadian rhythms, and oscillations in chemical reactions (e.g., the Belousov-Zhabotinsky (BZ) reaction). We focused on synchronization, which is when varying oscillations normalize to the same frequency through interactions of numerous oscillatory elements. Synchronization is considered to be a phase transition of a non-equilibrium system.
The oscillation of each oscillator can be written as a differential equation. If the mutual interaction between oscillators is weak, then a system of differential equations can be used to describe the phases of the oscillators. This is known as a phase oscillator model. We used the following differential equation, in which a sine function is chosen as the interaction function:
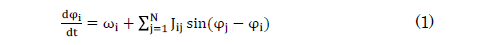
where φi is the phase of the ith oscillator, N is the number of oscillators, Jij is the strength of the interaction from the jth oscillator to the ith oscillator, ωi is the natural frequency of the ith oscillator, and g(ω) is the distribution of the natural frequency. If the natural frequency is constant and interactions are symmetric (i.e., Jij = Jji), then the system is equivalent to the classical XY model ( for magnets) at the temperature 0 with the same interactions as the oscillator network. This was the starting point of our research.
Kuramoto analytically solved the system with uniform interactions described by Equation (1) and demonstrated the existence of the synchronizationdesynchronization transition for the first time. This system is now known as the Kuramoto model. In brief, the model shows that numerous oscillators with varying oscillations synchronize when the strength of the interaction is greater than a certain value or when the distribution of the natural frequency is smaller than a certain value. Our goal was to develop a solvable phase oscillator model that differs from the Kuramoto model. For this purpose, we focused on the one-dimensional system of a circle, in which each oscillator interacts with all other oscillators. In this case, the degrees of synchronization of the system, which are known as order parameters, consist of several complex numbers. The Kuramoto model has only one order parameter because the phase of the single existing complex order parameter naturally disappears, and only its amplitude remains. However, the present model must also calculate the phase component of the complex order parameter. Meanwhile, the XY model, which has the same interactions as the present model, can be solved within the framework of classical statistical mechanics. Thus, we utilized the phase information for this model. While this approach was a detour, we also studied the XY model as a means of solving our problem. The results suggested that this was a very creative detour. We determined the phase by solving the equations of the XY model and used this information to solve the amplitude equation for an oscillator network and draw a phase diagram (shown below on the right).
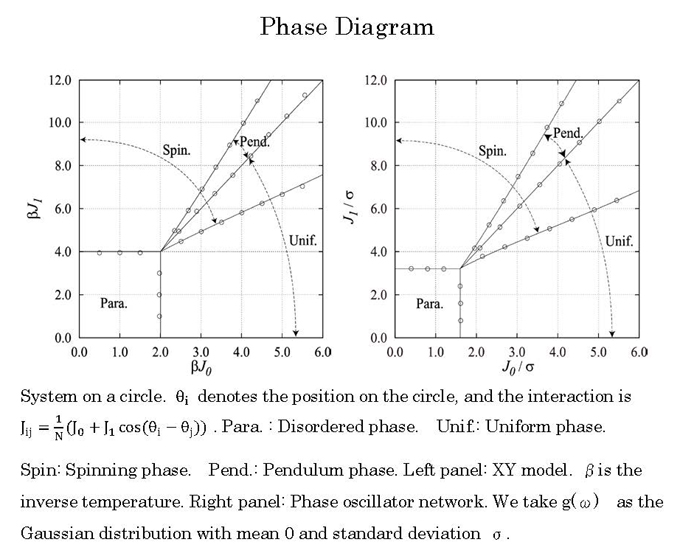
We also drew a phase diagram for the XY model, as shown on the left. The diagrams for both systems are rather similar, as are their amplitude equations. Furthermore, we derived and solved the phase boundary equations, which are also similar. At the time, we did not consider this discovery to be meaningful and received no comments when we presented the results in a meeting of the Physical Society of Japan. However, we later found a method to derive the equation for the phase part of the oscillator network. As always, things seemed obvious once we understood them. To our astonishment, the phase equations of the two systems were also similar. We were able to find the correspondence between the phase transition points for the two models and observed that the fluctuations of the natural frequency and temperature also corresponded. We surmised that the solutions to the equations for the order parameters in both systems may also correspond. After several trials and errors, we were able to prove mathematically that the solutions also corresponded one-to-one for each of the three ordered phases. The phase boundary equations also agreed. We proceeded to find interactions for which the correspondence existed and showed that the equations agreed one-to-one for a certain class of systems in which all elements interact with each other. The correspondence of solutions was also observed in several cases. These results were published in the Journal of the Physical Society of Japan in February 2015, and our paper was ranked among the top 20 most downloaded articles for February 2015 among the papers published in the journal since its foundation in 1946.
Although we were aware of some cases of creative mistakes, and many innovative detours certainly occur, this was our first experience of an unexpected discovery resulting from a detour.
[1] Correspondence between Phase Oscillator Network and Classical XY model with the Same Infinite-Range Interaction in Statics
Tatsuya Uezu, Tomoyuki Kimoto, Shuji Kiyokawa, and Masato Okada J. Phys. Soc. Jpn. 84, 033001 (2015)