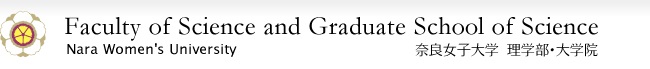Students in the Department of Mathematical and Physical Sciences learn the basics of either mathematics or physics and various methodologies. Moreover, students learn skills to express theories of mathematics and physics, such as the technique of computer programming. Opportunities to experience mathematics and physics actually applied in society are also offered.
Students who focus on physics do not simply learn about space, subatomic particles, and matter in the world around us, which have been the subjects of physics research up until now; they also get a chance to learn within fields concerning the nanometer-size system (also called the mesoscopic system in the sense of an intermediate between micro and macro). In addition, students learn about new fields from a physics-based perspective which deal with not only objects but also events such as information. These fields are the fundamental studies of so-called nano-technology, and they are closely related to the mechanisms of memory and recollection of the brain. There are also efforts to employ education on numerical simulation using computers as a method to study these fields and plasma phenomena, such as the aurora borealis.

The Physics and Mathematics Course involves education with the cooperation of mathematics and physics teachers with the aim of helping students acquire a balanced understanding of the two subjects. Specifically, students are first given a wide range of knowledge regarding mathematics and physics along with computer programming technique through lectures, experiments, seminars, and other means. Subsequently, graduation research involves learning a wide range of problem-solving and communication skills through seminars which deal with topics in mathematics and physics that are slightly different from what students have learned up by then.
This course features a new type of education forged through the cooperation of mathematics and physics teachers. Fourth-year students are not only grouped into laboratories studying the fields of traditional mathematics, physics, and information and computer sciences; they can also carry out their graduation research under new themes which constitute a bridge between these fields.

Nano electrons system theory (Hideo Yoshioka)

Graphene is the very thin planer material of carbon atoms in honeycomb structure. Motions of the electrons in this material are same as the massless ones in vacuum. I study theoretically their interesting phenomena such as magnetism and conduction.

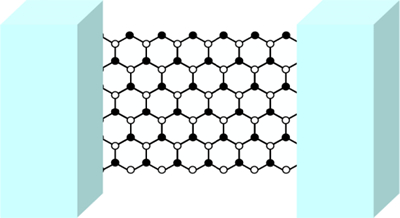
Theoretical study of electronic states in crystals (Masahisa Tsuchiizu)

Molecular conductors are crystals where the constituent units are molecules, and there are a full variety of electronic states owing to the various combinations of molecular species and their arrangement in crystals. The aim of my research is to elucidate the fundamental concepts of these phenomena theoretically.

Nonlinear Dynamics (So Kitsunezaki)

Complex dynamics hidden in natural phenomena often make intriguing patterns and motions. We study deformation and fracture of soft materials, patterns of collective motions created by microorganisms, and so on, both theoretically and experimentally.

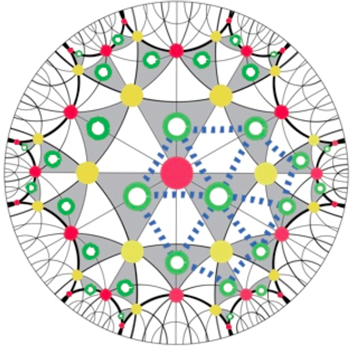
Group Theory and Discrete Geometry (Junichi Matsuzawa)

I am a mathematician working in group theory. My interest range from representation theory of groups to the mathematical study of symmetries of geometric structures appearing in the realm of nature such as liquid crystalline matters, surfactants, mitochondria, pigment cells of retina, chloroplasts, butterfly wing scales, etc.