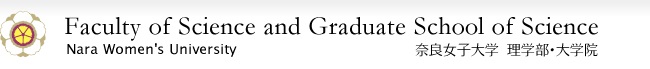[Release: January, 2016]
Associate Professor Shuji Kiyokawa
Physics Course & Physics and Mathematics Course
Department of Mathematical and Physical Sciences
Faculty of Science
Nara Women’s University

•What is a Plasma?
Raising the temperature turns ice into water, which eventually becomes steam. In other words, the state changes from solid to liquid to gas (see below).

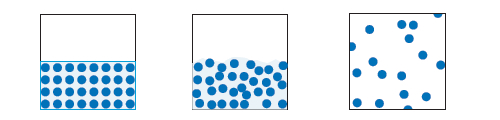
If the temperature is raised further, water molecules dissociate into hydrogen and oxygen atoms, both of which ionize at even higher temperatures. These atoms are called ionized gas when the degree of ionization is small, but they become a plasma when they are nearly 100% ionized at a greater temperature.

Plasmas can be observed in outer space, in stars such as the Sun, in auroras, but also in neon tubes. Plasma is characterized by a spontaneous phenomenon called plasma oscillation and another phenomenon in which ion charges are weakened by freely moving electrons surrounded them screening effect).

•Strongly Coupled Plasma

While the aforementioned plasma is dilute one, or very low density, increasing the density while maintaining the plasma state creates a strongly coupled plasma. Examples of strongly coupled plasmas include the plasma in the interior of stars and giant planets, such as Jupiter and Saturn, and the conduction electrons in metals.
An idealized model of a plasma is called one-component plasma (OCP). The properties of an OCP can be identified by the coupling constant G alone, which is defined as

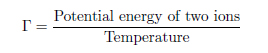
where G > 1 indicates a strongly coupled plasma.

Our research group studies this strongly coupled plasma.

•Phase Transitions in OCPs

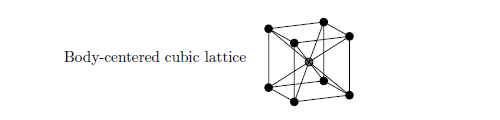
It has been discovered by computer simulations that a plasma goes through a phase transition and crystallizes when the coupling constant G value reaches approximately 172. At this point, the crystal structure is a body-centered cubic lattice (bcc). The structure of a bcc is shown in the following figure, where the black and gray circles represent the positions of the atoms, with lines drawn to connect the atoms and help visualize the structure. A crystal is formed when these cubes are precisely aligned vertically and horizontally.

♦Structure of White Dwarfs

A white dwarf is the final evolutionary state of stars with mass less than about 8 times the mass of the Sun. It is similar in size to the Earth but has a very high density and consists primarily of carbon and oxygen atoms, and there are some types of white dwarfs according to mixing ratio of carbon, oxygen and other elements.
The coupling constant of white dwarfs ranges between G = 100-200. Additionally, their bodies may contain a solid component. For example, the structure of a white dwarf in which carbon (C) and oxygen (O) form a strongly coupled plasma may look like that shown in the following figure.

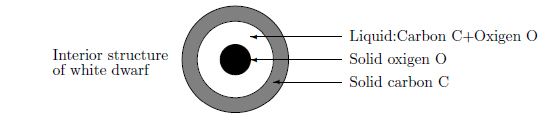
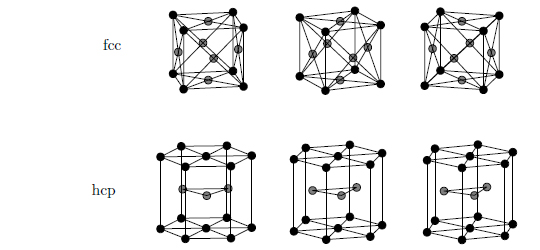
The radius of each phase is unknown. For OCPs, the crystal structure besides bcc has been predicted to transition to a face-centered cubic lattice (fcc), hexagonal close- packed (hcp), or simple cubic lattice (sc) structure, as shown below; however, such a behavior is yet to be verified.

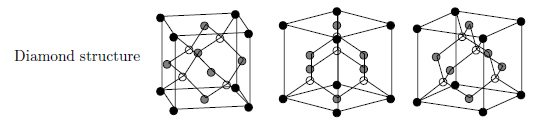
The coupling constant at the center of a white dwarf is likely to be very large (G>>172) and the crystal structure may not necessarily be a bcc; however, this also remains largely unknown. In the case of carbon, a terrestrial super-pressurized experiment using a diamond anvil showed that the ß-tin and SC4 crystal structures and the diamond structure can be produced.

♦Molecular Simulations by Parallel Computers
We are currently investigating whether strongly coupled carbon plasmas form an hcp or a diamond structure by simulating the environment of white dwarfs using computers. This is performed using a calculation method called molecular simulation, which requires an enormous amount of calculations. For this purpose, we have developed a distributed memory parallel computer (see the photo above).

Recent Publications Related to this Research

S.Kiyokawa
"Multi-average ion model for hot dense plasmas derived from finite temperature density-functional theory"
High Energy Density Physics 13:40-54 (2014).
http://www.sciencedirect.com/science/article/pii/S1574181814000603